힙

∙ 힙 (heap)

- heap 더미, 무더기, 퇴적물, (무엇인가를 차곡차곡) 쌓아 올린다.

- 자료 구조에서 힙은 완전 이진트리의 한 형태로서 힙 속성을 만족하는 자료 구조. 이진 힙 (binary heap)

- 힙 속성 (heap property)

> 최대 힙 속성 (max heap property) : 부모 노드의 키 값은 항상 자식 노드의 키 값보다 크거나 같다.

> 최소 힙 속성 (min heap property) : 부모 노드의 키 값은 항상 자식 노드의 키 값보다 작거나 같다.

 

∙ 힙의 특징

- 루트 노드는 항상 최댓값 또는 최솟값을 가짐

- 부모 - 자식 사이의 크기 관계만 있고, 왼쪽 자식 - 오른쪽 자식 사이의 크기 관계는 없음

- 완전 이진트리이기 때문에 트리의 높이는 h = [log2 n] (log 작은 2 n이다) 

- 힙의 응용 분야 : 힙 정렬, 우선순위 큐, 다익스트라 알고리즘 등

 

∙힙 연산의 시간 복잡도

- 최댓값 또는 최솟값 참조 : O(1)

- 원소 삽입 : O(log N)

- 원소 삭제 : O(log N)

 

∙ 힙과 이진 탐색 트리 차이

 

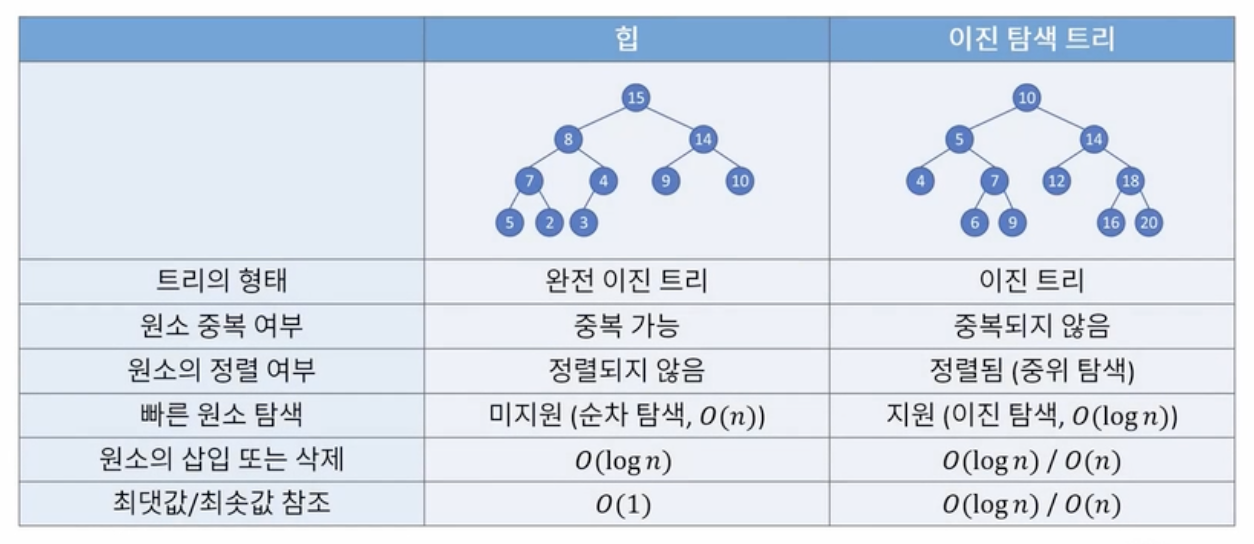
 ∙ 힙 구현

- 힙은 완전 이진트리이므로 각 노드에 인덱스 (index)를 붙이고, 배열을 이용하여 쉽게 표현할 수 있음

- 구현의 편의상 루트 노드의 인덱스를 1부터 시작 (배열의 0번 인덱스는 무시)

 

∙ 힙에 원소 삽입

1. 힙의 맨 마지막에 새로운 원소 값을 갖는 노드를 추가한다.

2. 새로 삽입한 노드와 부모 노드를 서로 비교하여 힙 속성을 만족하지 않으면 현재 노드와 부모 노드를 교환한다. 그리고 부모 노드에서 이 작업을 반복한다.

 

∙ 힙에서 원소 삭제

1. 힙의 맨 마지막 노드 값을 루트 노드로 복사하고, 맨 마지막 노드를 삭제한다.

2. 루트 노드와 두 자식 노드를 비교하여 힙 속성을 만족하지 않으면 두 자식 노드 중에서 더 큰(최대 힙) 노드와 서로 교환한다. 그리고 교환한 노드에서 이 작업을 반복한다.

 

 

∙소스 코드

#include <algorithm>
#include <iostream>
#include <vector>

using namespace std;

class MaxHeap
{
private:
    vector<int> vec;

public:
    MaxHeap() : vec(1) {}

    void push(int value)
    {
        vec.push_back(value);
        heapify_up(vec.size() - 1);
    }

    void pop()
    {
        vec[1] = vec.back();
        vec.pop_back();
        heapify_down(1);
    }

    int top() const { return vec[1]; }

    void clear() { vec.clear(); vec.push_back(0); }
    int size() { return vec.size() - 1; }
    bool empty() { return vec.size() == 1; }

    void print()
    {
        for (auto n : vec)
            cout << n << ", ";
        cout << endl;
    }

private:
    int parent(int i) { return i / 2; }
    int left(int i) { return 2 * i; }
    int right(int i) { return 2 * i + 1; }

    void heapify_up(int i)
    {
        if (i > 1 && vec[i] > vec[parent(i)]) {
            swap(vec[i], vec[parent(i)]);
            heapify_up(parent(i));
        }
    }

    void heapify_down(int i)
    {
        int largest = i;

        if (left(i) < vec.size() && vec[left(i)] > vec[largest]) {
            largest = left(i);
        }

        if (right(i) < vec.size() && vec[right(i)] > vec[largest]) {
            largest = right(i);
        }

        if (largest != i) {
            swap(vec[i], vec[largest]);
            heapify_down(largest);
        }
    }
};

int main()
{
    MaxHeap heap;
    heap.push(10);
    heap.push(5);
    heap.push(15);
    heap.push(7);
    heap.push(3);
    heap.push(9);
    heap.push(14);
    heap.push(8);
    heap.push(2);
    heap.push(4);
    heap.print();

    while (!heap.empty()) {
        cout << heap.top() << ", ";
        heap.pop();
    }
    cout << endl;
}