트리과 이진 트리
∙ 트리 (tree)

- 계층적인 구조를 나타내는 자료 구조
- 보통 뿌리가 위에, 나뭇가지와 잎이 아래로 자라는 형태로 표현
∙ 트리의 구성 요소

- 노드 (node, vertex)
> 트리의 데이터를 저장하는 원소 단위
- 에지 (edge, link)
> 노드와 노드를 연결하는 선
> 트리의 에지는 부모-자식 계층 관계만을 나타냄
> 노드의 개수가 N이면 항상 N - 1개의 에지가 존재
∙ 이진트리

- 모든 노드가 최대 두 개의 자식을 갖는 트리
> 모든 노드의 차수가 2 이하인 트리
> 모든 노드가 2개의 서브트리를 가지고 있는 트리 (서브트리는 빈 트리(empty tree) 일 수 있음)
- 각각의 자식 노드는 부모의 왼쪽 자식 또는 오른쪽 자신으로 지정됨
∙ 정 이진트리 (proper binary tree, full binary tree)

- 모든 노드가 0개 또는 2개의 자식 노드를 갖는 이진 트리 (리프 노드를 제외한 노드들은 모두 자식이 2개임)
∙ 포화 이진 트리 (perfect binary tree)

- 트리의 모든 레벨에서 노드가 모두 채워져 있는 이진 트리
- 높이가 h이면 노드 개수가 2^h+1 - 1
∙ 완전 이진 트리 (complete binary tree)

- 마지막 레벨을 제외한 모든 레벨에는 노드가 완전히 채워져 있고, 마지막 레벨에는 노드가 왼쪽부터 채워져 있는 이진 트리
∙ 균형 이진 트리 (balaneced binary tree)

- 모든 노드의 서브 트리 간의 높이 차이가 1 이하
∙ 편향 트리 (skewed tree)

- 리프 노드를 제외한 모든 노드가 하나의 자식 노드만 갖는 트리
∙ 이진트리 구현 방법
- 제열
> 완전 이진트리의 경우, 배열을 이용하여 효율적으로 표현 가능
- 연결 리스트
> 저장할 데이터와 왼쪽 자식과 오른쪽 자식 노드를 가리키는 포인터 2개를 갖는 구조체를 사용
- 이진 트리 구현 소스 코드

int main()
{
Node* root = new Node('A');
root -> left = new Node('B');
root -> reight = new Node('C');
root -> root -> left = new Node('D');
root -> root -> right = new Node('E');
root -> root -> right = new Node('F');
}
∙ 트리 순회
- 정해진 순서에 의해 트리의 모든 노드를 (한 번씩) 방문하는 작업
- 전형적인 트리 순회 방법
> 전위 순회 (preoder traversal)
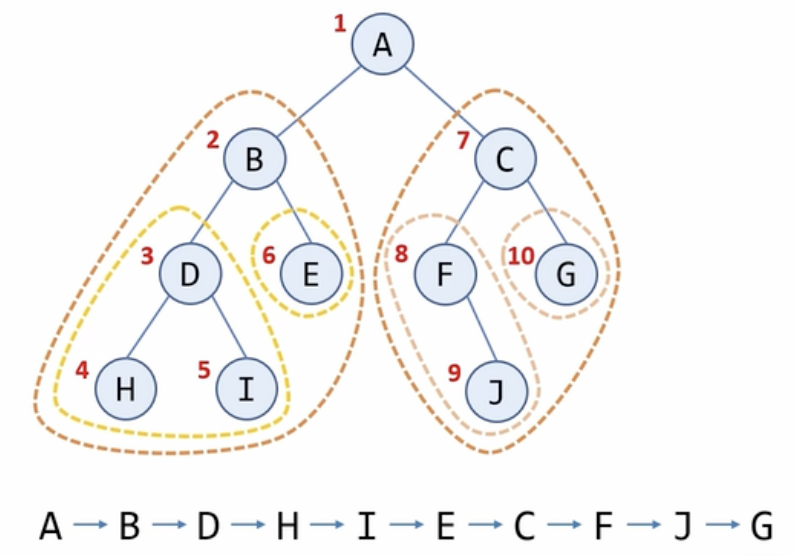
void preorder(Node* node)
{
if (node) {
cout << node -> data << ", ";
preorder(node -> left);
preorder(node -> right);
}
}
> 중위 순회 (inorder traversal)
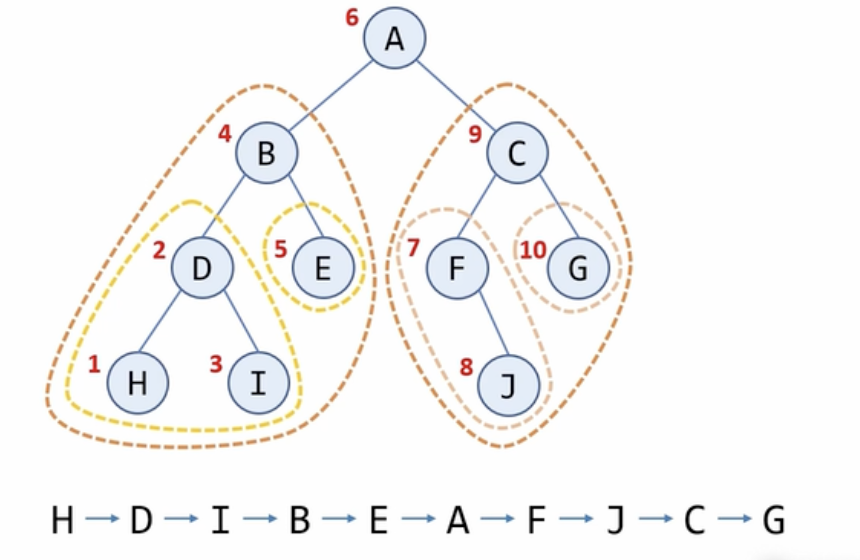
void inorder(Node* node)
{
if (node){
inorder(node -> left);
cout << node -> data << ", ";
inorder(node -> right);
}
}
> 후위 순회 (postorder traversal)

void postorder(Node* node)
{
if (node) {
postorder(node -> left);
postorder(node -> right);
cout << node -> data << ", ";
}
}
> 레벨 순서 순회 (level order traversal)
- 낮은 레벨에 있는 노드를 모두 방문한 후, 큰 레벨로 이동하여 방문을 바이복
- 큐를 사용하여 구현

void levelorder(Node* node)
{
std::queue<Node*> q;
q.push(node);
while (!q.empty()) {
auto curr = q.front();
q.pop();
std::cout << curr -> data << ", ";
if (curr -> left)
q.push(curr -> left);
if (curr -> right)
q.push(cur -> right);
}
}
> 이진트리 삭제
- 각각의 노드에서 왼쪽 자식 노드와 오른쪽 자식 노드를 먼저 삭제하고, 자기 자신을 삭제하는 코드를 재귀적으로 수행
void delete_tree(Node* node)
{
if (node)
delete_tree(node -> left);
delete_tree(node -> right);
delete node;
}
> 전체 소스 코드
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
// 트리를 만들기 위하 Node 구조체 정의
struct Node
{
char data;
Node* left;
Node* right;
Node(char d) : data(d), left(nullptr), right(nullptr) {};
};
// 전위 순회
void preorder(Node* node)
{
if (node){
cout << node -> data << ", ";
preorder(node -> left);
preorder(node -> right);
}
}
// 중위 순회
void inorder(Node* node)
{
if (node){
inorder(node -> left);
cout << node -> data << ", ";
inorder(node -> right);
}
}
// 후위 순회
void postorder(Node* node)
{
if (node){
postorder(node -> left);
postorder(node -> right);
cout << node -> data << ", ";
}
}
// 레벨 순회
void levelorder(Node* node)
{
queue<Node*> q;
q.push(node);
while (!q.empty()) {
auto curr = q.front();
q.pop();
cout << curr -> data << ", ";
if (curr -> left)
q.push(curr -> left);
if (curr -> right)
q.push(curr -> right);
}
}
// 이진 트리 삭제
void delete_tree(Node* node)
{
if (node)
delete_tree(node -> left);
delete_tree(node -> right);
delete node;
}
int main()
{
Node* root = nullptr;
root = new Node('A');
root -> left = new Node('B');
root -> right = new Node('C');
root -> left -> left = new Node('D');
root -> left -> right = new Node('E');
root -> right -> right = new Node('F');
preorder(root); cout << endl;
inorder(root); cout << endl;
postorder(root); cout << endl;
levelorder(root); cout << endl;
delete_tree(root);
}

