이진 탐색 트리
∙ 이진 탐색 트리 (BST : binary search tree)

- 효율적인 자료의 탐색을 위한 이진트리 기반의 자료구조
> 자료의 계층적인 구조를 표현하기 위해 트리를 사용하는 것이 아니라, 자료의 효율적인 관리를 위해 트리 구조를 사용
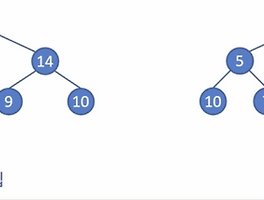
- 모든 노드 N에 대해 왼쪽 서브트리에 있는 모든 노드의 키(key) 값은 노드 N의 키 값보다 작고, 오른쪽 서브트리에 있는 모든 노드의 키 값은 노드 N의 키 값보다 크다
∙ 이진 탐색 트리의 특징
- 자료의 탐색, 삽입, 삭제가 모두 O(log n) 시간 복잡도로 동작
- 이진 탐색 트리를 중위순회하면 오름차순으로 정렬된 값을 얻을 수 있음
∙ 이진 탐색 트리에서 탐색
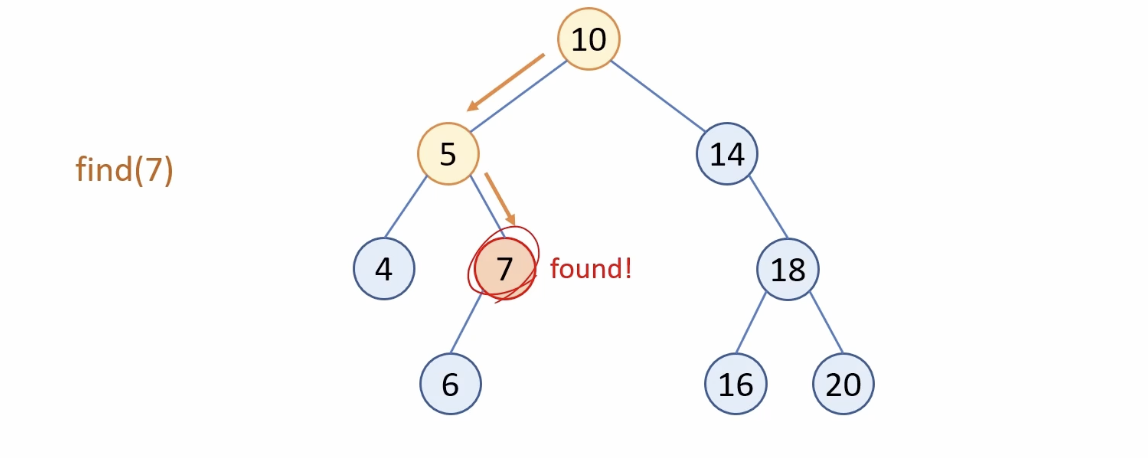
- 소스 코드
#include <iostream>
#include <vector>
using namespace std;
// 트리를 만들기 위한 Node 구조체
struct Node
{
int data;
Node* left;
Node* right;
Node(int d) : data(d), left(nullptr), right(nullptr) {}
};
//
class BinarySearchTree
{
private:
Node* root = nullptr;
public:
// 소멸자부분에서는 전체 트리를 삭제하는 코드
~BinarySearchTree()
{
delete_tree(root);
}
// 새로운 데이터 추가하는 코드
void insert(int value)
{
if (!root)
root = new Node(value);
else
insert_impl(root, value);
}
// 특정 데이터를 찾는 코드
Node* find(int value)
{
return find_impl(root, value);
}
// 중위순회 방식으로 방문하면서 각각의 데이터값들을 출력하는 코드
void inorder()
{
inorder_impl(root);
}
private:
void insert_impl(Node* curr, int value)
{
if (value < curr->data) {
if (!curr->left)
curr->left = new Node(value);
else
insert_impl(curr->left, value);
} else {
if (!curr->right)
curr->right = new Node(value);
else
insert_impl(curr->right, value);
}
}
Node* find_impl(Node* curr, int value)
{
if (curr == nullptr)
return nullptr;
if (value == curr->data)
return curr;
else {
if (value < curr->data)
return find_impl(curr->left, value);
else
return find_impl(curr->right, value);
}
}
void inorder_impl(Node* curr)
{
if (curr) {
inorder_impl(curr->left);
std::cout << curr->data << ", ";
inorder_impl(curr->right);
}
}
void delete_tree(Node* node)
{
if (node) {
delete_tree(node->left);
delete_tree(node->right);
delete node;
}
}
};
int main()
{
// 트리 생성
BinarySearchTree bst;
bst.insert(10);
bst.insert(14);
bst.insert(5);
bst.insert(7);
bst.insert(18);
bst.insert(4);
bst.insert(6);
bst.insert(20);
bst.insert(16);
bst.inorder(); cout << endl;
// 생성된 트리에서 특정 데이터 탐색
if (bst.find(7))
cout << "7 is found" << endl;
else
cout << "7 is not found" << endl;
if (bst.find(15))
cout << "15 is found" << endl;
else
cout << "15 is not found" << endl;
// 생성된 트리에 데이터 추가
bst.insert(9);
bst.insert(12);
bst.inorder(); cout << endl;
}
∙ 이진 탐색 트리에서 삭제
- 이진 탐색 트리에서 자료의 삭제는 해당 노드를 삭제한 후, BST속성을 만족할 수 있는 다른 적절한 노드를 찾아 해당 노드로 대체해야 함
Case1. 자식 노드가 없는 경우 : 해당 노드를 삭제하고 링크를 제거
Case2. 자식 노드가 하나만 있는 경우 : 해당 노드를 삭제하고, 부모 노드의 포인터가 해당 노드의 자식 노드를 가리키도록 설정
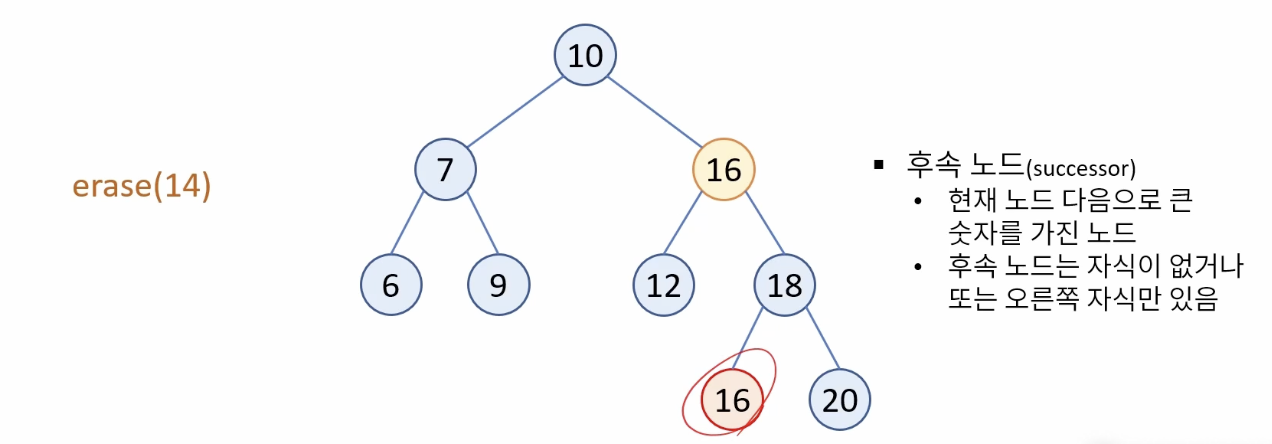
Case3. 자식 노드가 두 개 있는 경우 : 후속 노드의 값을 현재 노드로 복사하고, 후속 노드를 삭제
* 후속 노드 (successor) :
현재 노드 다음으로 큰 숫자를 가진 노드 (현재 노드의 오른쪽 서브 트리에서 가장 작은 값의 노드)
class BinarySearchTree
{
private:
Node* root = nullptr;
public:
void erase(int value)
{
root = erase_impl(root, value);
}
private:
// 노드 삭제 후, 부모 노드 포인터가 가리켜야 함
// 노드의 주소를 반환
Node* erase_impl(Node* node, int value)
{
// node가 NULL일 경우 그대로 출력
if (node)
return nullptr;
// 삭제할려는 값이 현제 가리키고 있는 키값 보다 작으면 왼쪽 노드로 이동 후, 재귀호출
if (value < node -> data)
node -> left = erase_impl(node -> left, value);
// 오른쪽 노드로 이동 후, 재귀호출
else if (value > node -> data)
node -> right = erase_impl(node -> right, value);
else
if (node->left && node->right) {
// 자식 노드가 둘 다 있는 경우
auto succ = successor(node);
node->data = succ->data;
node->right = erase_impl(node->right, succ->data);
}
else {
// 자식 노드가 전혀 없거나, 한쪽 자식만 있는 경우
auto tmp = node->left ? node->left : node->right;
delete node;
return tmp;
}
}
return node;
}
- 전체 소스 코드
#include <iostream>
#include <vector>
using namespace std;
struct Node
{
int data;
Node* left;
Node* right;
Node(int d) : data(d), left(nullptr), right(nullptr) {}
};
class BinarySearchTree
{
private:
Node* root = nullptr;
public:
~BinarySearchTree()
{
delete_tree(root);
}
void insert(int value)
{
if (!root)
root = new Node(value);
else
insert_impl(root, value);
}
Node* find(int value)
{
return find_impl(root, value);
}
void inorder()
{
inorder_impl(root);
}
void erase(int value)
{
root = erase_impl(root, value);
}
private:
void insert_impl(Node* curr, int value)
{
if (value < curr->data) {
if (!curr->left)
curr->left = new Node(value);
else
insert_impl(curr->left, value);
} else {
if (!curr->right)
curr->right = new Node(value);
else
insert_impl(curr->right, value);
}
}
Node* find_impl(Node* curr, int value)
{
if (curr == nullptr)
return nullptr;
if (value == curr->data)
return curr;
else {
if (value < curr->data)
return find_impl(curr->left, value);
else
return find_impl(curr->right, value);
}
}
void inorder_impl(Node* curr)
{
if (curr) {
inorder_impl(curr->left);
std::cout << curr->data << ", ";
inorder_impl(curr->right);
}
}
Node* successor(Node* node)
{
auto curr = node->right;
while (curr && curr->left)
curr = curr->left;
return curr;
}
// 노드 삭제 후, 부모 노드 포인터가 가리켜야 할 노드의 주소를 반환
Node* erase_impl(Node* node, int value)
{
if (!node)
return nullptr;
if (value < node->data)
node->left = erase_impl(node->left, value);
else if (value > node->data)
node->right = erase_impl(node->right, value);
else {
if (node->left && node->right) {
// 자식 노드가 둘 다 있는 경우
auto succ = successor(node);
node->data = succ->data;
node->right = erase_impl(node->right, succ->data);
} else {
// 자식 노드가 전혀 없거나, 한쪽 자식만 있는 경우
auto tmp = node->left ? node->left : node->right;
delete node;
return tmp;
}
}
return node;
}
void delete_tree(Node* node)
{
if (node) {
delete_tree(node->left);
delete_tree(node->right);
delete node;
}
}
};
int main()
{
BinarySearchTree bst;
bst.insert(10);
bst.insert(14);
bst.insert(5);
bst.insert(7);
bst.insert(18);
bst.insert(4);
bst.insert(6);
bst.insert(20);
bst.insert(16);
bst.inorder(); cout << endl;
if (bst.find(7))
cout << "7 is found" << endl;
else
cout << "7 is not found" << endl;
if (bst.find(15))
cout << "15 is found" << endl;
else
cout << "15 is not found" << endl;
bst.insert(9);
bst.insert(12);
bst.inorder(); cout << endl;
bst.erase(4);
bst.erase(5);
bst.erase(14);
bst.inorder(); cout << endl;
bst.insert(15);
bst.erase(10);
bst.inorder(); cout << endl;
}
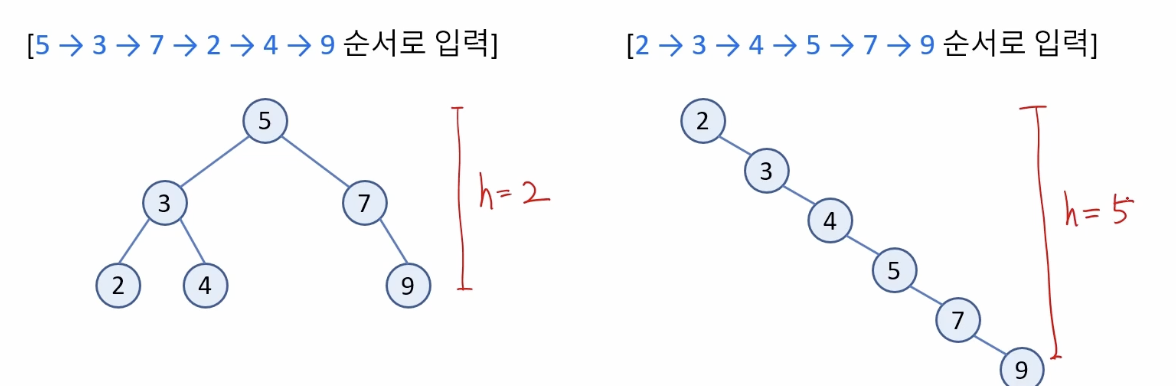
∙ 이진 탐색 트리의 문제점
- 원소의 삽입 순서에 따라 이진 탐색 트리가 한쪽으로 치우친 형태로 구성될 수 있음
- 트리가 한쪽으로 치우칠 경우, 트리의 높이가 h = n - 1 형태로 구성되므로, 탐색, 삽입, 삭제 연산의 시간 복잡도가 O(n)으로 결정됨
∙ 이진 탐색 트리의 문제점 해결 방법
- 한쪽으로 치우친 트리의 구성을 변경하여 균형 잡힌 트리 형태로 변경할 수 있음
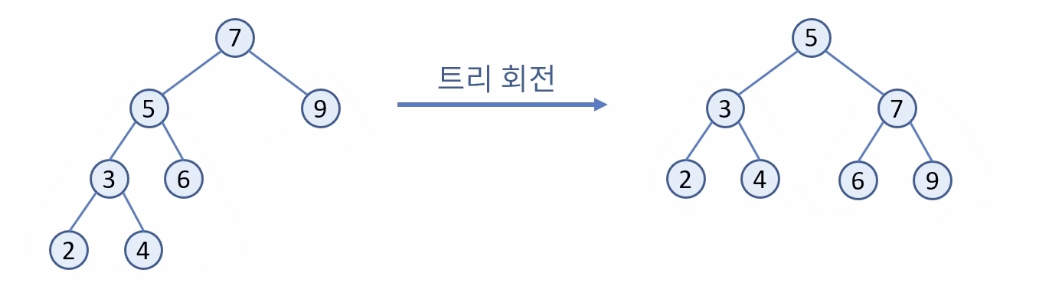
- 균형 잡힌 트리의 예
> AVL 트리, 레드-블랙 트리, B트리, 스플레이 트리 등
∙ std::set 과 std::map
- set 과 map 차이
> set은 키(key)만 저장
> map은 키(key)와 값(value)을 저장
- set과 muliset 차이
> set은 고유한 키의 데이터만 저장 (중복 허용 안함)
> multiset은 중복되는 데이터를 저장
- set과 unordered_set 차이
> set은 내부에서 데이터를 정렬해서 저장
> unordered_set은 데이터를 정렬하지 않음
∙ std::set 컨테이너
- Key 타입의 키 값을 저장하는 연관 컨테이너
- 저장된 데이터는 키 값을 기준으로 정렬됨
- 데이터 삽입, 삭제, 탐색은 O(log n) 시간 복잡도로. 동작
- 보통 레드-블랙 트리를 이용하여 구현됨
- 만약 중복되는 데이터를 set구조로 저장하려면 std::multiset 컨테이너를 사용
- 만약 데이터를 정렬되지 않은 상태로 저장하려면 std::unordered_set 컨테이너를 사용
- 사용자 정의 타입을 저장할 경우, 비교 연산을 지원해야 함
- <set>에 정의되어 있음
| 멤버 함수 | 설명 |
| begin(), end() rbegin(), rend() |
순방향 및 역방향 반복자 반환 |
| insert() | (중복되지 않는) 새로운 원소를 삽입 |
| erase() | 특정 원소를 삭제 |
| find() | 특정 키 값을 갖는 원소를 찾아 반복자를 반환. 원소를 끝까지 찾지 못하면 end()에 해당하는 반복자를 반환 |
| clear() | 모든 원솔ㄹ 삭제 |
| size() | 원소의 개수를 반환 |
| empty() | set이 비어 있으면 true를 반환 |
#include <iostream>
#include <set>
#include <string>
using namespace std;
int main()
{
set<int> odds; // 홀수 값 저장
// greater 값을 지정하면 내림차순으로 정렬됨
set<int, greater<>> evens {2,4,6,8}; // 짝수 값 저장
evens.insert(10);
evens.insert(2); // 중복이 되어 생략됨
// 임의로 데이터를 넣어도 오름차순으로 정렬되어 있음
odds.insert(1);
odds.insert(7);
odds.insert(5);
odds.insert(3);
odds.insert(9);
for (auto n : odds)
cout << n << ", ";
cout << endl;
for (auto n : evens)
cout << n << ", ";
cout << endl;
// 특정 데이터 값 찾기
if (evens.find(4) != evens.end())
cout << "4 is found!" << endl;
else
cout << "4 is not found!" << endl;
// 문자열과 정수값을 쌍으로 이루어진 데이터를 저장하고 싶을 경우
// set<pair<string, int>> managers = {{"Amelia", 29}, {"Noah", 25}, {"Olivia", 31}, {"Sophia", 40}};
using psi = pair<string, int>;
set<psi> managers = {{"Amelia", 29}, {"Noah", 25}, {"Olivia", 31}, {"Sophia", 40}};
// 데이터 삽입
managers.insert({"George", 35});
// 특정 데이터 찾기
psi person1 = {"Noah", 25};
if (managers.find(person1) != managers.end())
cout << person1.first << "is a manager!" << endl;
else
cout << person1.first << "is not a manager!" << endl;
// 특정 데이터 삭제
managers.erase({"Sophia", 40});
managers.erase({"Noah", 30}); // 30살의 Noah는 없기 때문에 삭제가 안됨
for (auto m : managers)
cout << m.first << "(" << m.second << ")" << ", ";
}
∙ std::map 컨테이너
- Key 타입의 키와 T타입의 값의 쌍을 저장하는 연관 컨테이너
- 저장된 데이터는 키 값을 기준으로 정렬됨
- 데이터 삽입, 삭제, 탐색은 O(log n) 시간 복잡도로 동작
- 보통 레드-블랙 트리를 이용하여 구현됨
- 만약 중복되는 데이터를 set구조로 저장하려면 std::multiset 컨테이너를 사용
- 만약 데이터를 정렬되지 않은 상태로 저장하려면 std::unordered_set 컨테이너를 사용
- 사용자 정의 타입을 저장할 경우, 비교 연산을 지원해야 함
- <map>에 정의되어 있음
| 멤버 함수 | 설명 |
| begin(), end() rbegin(), rend() |
순방향 및 역방향 반복자 반환 |
| insert() | (중복되지 않는) 새로운 원소를 삽입 |
| erase() | 특정 원소를 삭제 |
| find() | 특정 키 값을 갖는 원소를 찾아 반복자를 반환. 원소를 끝까지 찾지 못하면 end()에 해당하는 반복자를 반환 |
| clear() | 모든 원솔ㄹ 삭제 |
| size() | 원소의 개수를 반환 |
| empty() | map이 비어 있으면 true를 반환 |
| operator [] | 특정 키에 해당하는 원소의 값을 참조로 반환. 해당 키의 원소가 없으면 새로운 원소를 기본값으로 생성하여 참조를 반환 |
#include <iostream>
#include <string>
#include <map>
using namespace std;
int main()
{
// 자체적으로 정렬이 됨 (오름차순)
map<string, int> fruits;
// 데이터 삽입
fruits.insert({"apple", 1000});
fruits.insert({"banana", 1500});
// apple의 value 값이 출력
cout << fruits["apple"] << endl;
for (auto p : fruits)
cout << p.first << " is " << p.second << " Won. " << endl;
// 특정 데이터 값 수정
fruits["apple"] = 3000;
// 특정 데이터 삭제
fruits.erase("banana");
for (auto [name, price] : fruits)
cout << "2차 " << name << " is " << price<< " Won. " << endl;
}