∙ 동적 계획법 (dynamic programming)
- 복잡한 문제를 간단한 여러 개의 부분 문제로 나누고, 부분 문제에 대한 해답을 활용하여 전체 문제를 해결하는 문제 해결 방식
- 분할 정복법에서는 분할된 부분 문제들이 서로 겹치지 않지만, 동적 계획법에서는 중복되는 부분 문제가 발생한다는 점이 다름
- 보통 최적화 문제 또는 카운팅 문제에 적용
- 유명한 동적 계획법 문제
> 0-1 배낭 문제
> 부분집합의 합 문제
> 최장 공통부분 시퀀스
> 연쇄 행렬 곱셉
> 최소 비용 경로
∙ 동적 계획법 필요 조건
- 중복되는 부분 문제 (overlapping subproblems)
> 주어진 문제를 여러 개의 부분 문제로 분할할 경우, 몇몇 부분 문제가 반복되어 나타나는 현상
> 부분 문제의 솔루션을 저장하여 같은 부분 문제를 중복해서 계산하지 않도록 설정
- 최적 부분 구조 (optimal substructure)
> 부분 문제의 최적해를 조합하여 전체 문제의 최적해를 구할 수 있는 경우를 지칭
- 동적 계획법 문제의 해경 방법
> 기저 조건 정의
> 상태 전환을 나타내는 순환식 정의
> 순환식을 메모이제이션 또는 타뷸레이션 방식으로 풀이
∙ 피보나치수열 (Fibonacci squence)


- 첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열
- 1, 1, 2, 3, 5, 8, 13, 21, 34, 55....
- 편의상 0번째 항을 0으로 설정하기도 함
∙ 재귀 함수를 이용한 피보나치수열 계산
- 중복되는 부분 문제 발생
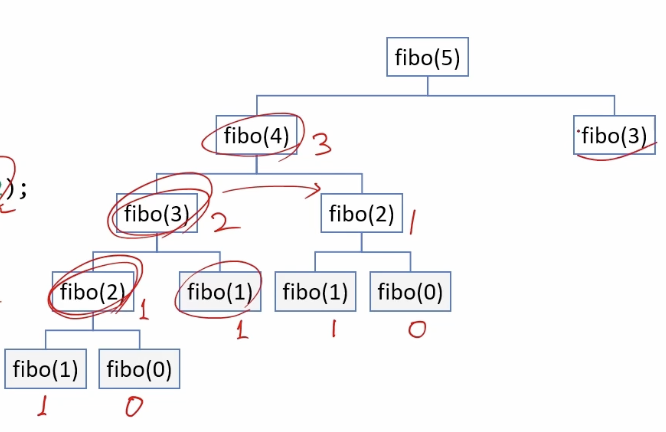
int fibo(int n)
{
if (n < 2)
return n;
return fibo(n - 1) + fibo(n - 2);
}
∙ 메모이제이션 (memoization)

- 중복 계산될 수 있는 값을 캐시에 저장하여 재사용
- 하향식 접근 방법
int fibo(int n)
{
if (n < 2)
reutrn n;
if (memo[n] != -1)
return memo[n];
memo[n] = fibo(n - 2) + fibo(n - 1);
return memo[n];
}
∙ 타뷸레이션 (tabulation)
- 모든 부분문제 연산 결과를 미리 표에 저장하여 사용하는 방식
- 상향식 접근 방법
int fibo(int n)
{
vector<int> dp(n + 1, 0);
dp[1] = 1;
for (int i = 2; i <= n; i++)
dp[i] = dp[i - 2] + dp[i - 1];
return dp[n];
}
∙ 메모이제이션 vs 타뷸레이션
| 메모이제이션 | 타뷸레이션 |
| 재귀 호출이 많이 발생하므로, 함수 호출에 따른 오버헤드가 있음 | 표에 저장된 값을 참조하는 방식이므로 빠르게 동작 |
| 경우에 따라 모든 부분 문제를 풀지 않아도 문제에 대한 해답을 구할 수 있음 | 상향식 방식이기 때문에 모든 부분 문제에 대한 해답을 구해서 표에 저장 |
| 캐시로 사용하는 표의 일부만 필요에 따라 계산하여 채움 | 표의 맨 처음부터 끝까지 차례대로 계산하여 모두 채움 |
- 전체 소스 코드
#include <iostream>
#include <vector>
using namespace std;
// 재귀함수를 이용함
int fibo1(int n)
{
if (n < 2)
return n;
return fibo1(n - 1) + fibo1(n - 2);
}
// 메모이제이션 기법
vector<int> memo(50, -1);
int fibo2(int n)
{
if (n < 2)
return memo[n];
memo[n] = fibo2(n - 2) + fibo2(n - 1);
return memo[n];
}
// 타뷸레이션 기법
int fibo3(int n)
{
vector<int> dp(n + 1, 0);
dp[1] = 1;
for (int i = 2; i <= n; i++)
dp[i] = dp[i - 2] + dp[i - 1];
return dp[n];
}
int main()
{
int n = 5;
cout << fibo1(n) << endl;
cout << fibo2(n) << endl;
cout << fibo3(n) << endl;
}'코딩 및 기타 > 어서와! 자료구조와 알고리즘' 카테고리의 다른 글
| 동적 계획법 응용 : 정수 삼각형 (0) | 2023.09.02 |
|---|---|
| 동적 계획법 응용 : 최소 비용 경로 (0) | 2023.09.01 |
| 그래프 순회 응용 (네트워크) (0) | 2023.09.01 |
| DFS 와 BFS (0) | 2023.08.31 |
| 그래프 (0) | 2023.08.30 |



